Git Diff 算法详解:Myers Diff Algorithm
Git Diff 算法详解:Myers Diff Algorithm
Diff日常
作为一个PROGRAMMER,可能每天你都在使用 Git 或 SVN 管理你所参与项目的代码。每当你提交自己修改后的代码、复读同事写的程序或排查程序异常行为的时候,比较和阅读两个版本代码之间的差异是必不可少的工作。
下图是 GitHub Desktop 展示的代码比对结果,我们可以很容易地看出:
- 左侧代表“旧”代码,右侧代表“新”代码。
- 左侧红色区域代表我们删除的代码,而右侧绿色区域代表我们新插入的代码
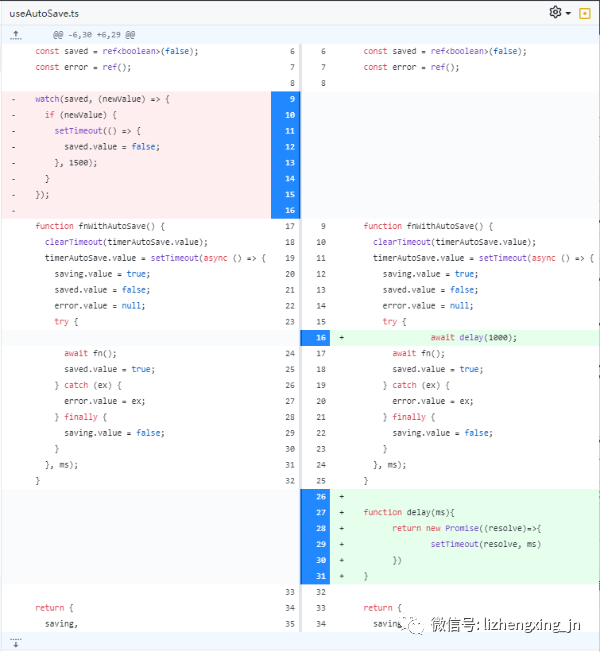
“代码比对”是 Git、SVN 这类代码版本管理软件中的基本的能力,也是最重要的能力。🚀️ (PS:代码合并的前提就是代码比对👀️ 。)
你知道“代码比对”是怎么做到的吗?😄 (PS:如果你心里已经有答案了,那就不用继续读这篇文章了👀️。)
Git内置的Diff算法
Git 是目前主流的版本控制系统,它的代码比对能力由 Git 内部的比对(Diff)算法实现。
Git 内置有 4 种 Diff 算法,即 Myers,Minimal,Patience 和 Histogram。其中 Myers 是 Git 使用的默认比对算法。我们可以在执行比对命令 git diff 时,通过参数 --diff-algorithm 指定比对算法。

下面,本文将选择 Git 的默认比对算法 Myers,为大家进行详细讲解。
Myers算法简介
Myers Diff Algorithm 是 Git 中的默认代码比对算法,由 Eugene W. Myers 在 1986 年发表。该算法的特点是运行速度快、生成的比对结果可读性强。
Myers 算法本质上是一个动态规划(Dynamic Programming,DP)算法,是一个“最短编辑距离(Minimum Edit Distance)”算法,也是一个“最长公共子序列(Longest Common Subsequence,LCS)”算法。
搞明白 Myers 算法不仅有利于你了解 Git 的底层工作原理,也有助于为你在解决一些工作中遇到的某些问题时提供灵感。
Myers 算法的原文很精练(如下图),想快速搞明白该算法的运行原理有一定难度。我用了两个周时间,反复读了好几遍这篇论文,并用 JavaScript 实现了一遍这个算法。我写这篇文章,一方面是想跟大家分享一下我对 Myers 算法的认识和理解,更重要的是希望能帮正在阅读本文的同学快速以更短的时间掌握 Myers 算法。

我们从论文中的例子开始,思考一下😄 。
主问题1:如何计算下面两个字符串 a 与 b 之间的“差异”?
a = ABCABBA
b = CBABAC子问题1.1:什么是“差异”?
答:“差异”是指,我们通过对字符串 a 中的字符进行一系列怎样的操作(注意:只有删除操作、插入操作),能把字符串 a 转换成 字符串 b。
举例子1.1:
一个最简单的“差异”就是,把字符串 a 中的字符逐个删除,然后把字符串 b 中的字符逐个插入。

很显然,这种“差异”对我们来说没有什么意义。想象一下,如果你在比对昨天和今天写的代码差异的时候,版本管理软件告诉你,“差异”是把昨天的代码全部删除、然后把今天的代码全部插入,完全没有意义好嘛😄 。
举例子1.2:
下图也是字符串 a、b 间的一种“差异”。它比上1.1版好很多,有点接近使用 Git、SVN 做比对的效果了。
因为它告诉我们,想要从字符串 a 变成字符串 b:
a = ABCABBA
b = CBABAC我们可以先从 a 字符串中删除开头的字符 A、B,然后保持字符 C 不动,然后插入字符 B,然后保持字符 A、B 不动,然后删除字符 B,然后保持字符 A 不动,最后插入字符 C。

举例子1.3:
下图所展示的也是字符串 a、b 间的“差异”,它们都是对的。

主问题2:什么样的“差异”更“好”?
我们一直在使用 Git 或 SVN 提供的代码比对功能,我们对“好”的差异比对结果有一种直觉,那就是“把修改过的内容原原本本地展示出来”。
但是从上面的例子中可以看出,对于 a、b 两个字符串间的“差异”,存在多种解释方式,那么我们应该选择什么样的解释,才能够贴近我们对“好”的理解。
在这里我们可以先总结几条规则:
- 涉及变动的部分尽量少(即:删除、插入操作尽量少)。
- 我们习惯看到,插入的部分在删除的部分后面。
- 我们习惯看到,成块的代码被删除或者被插入,而不是代码行交错地删除或插入。

- 我们习惯看到代码比对结果中所展示的“删除的代码”和“插入的代码”与我们的想法保持一致。

Myers 算法就是这样一种算法,它的运行速度快,而且能够在绝大多数场景下,产出较好的代码比对结果。
Myers算法流程
还是从论文中的例子开始,使用 Myers 算法找出下面字符串 a、b 间的差异。
a = ABCABBA
b = CBABAC不妨先看一下答案,下图即为 Myers 算法给出的差异比对结果😄 。

ok,进入正题。
图表示法
我们使用一张图(下图),对 a、b 两个字符串间的关系进行表达:
- 字符串 a,排列在水平方向上。
- 字符串 b,排列在竖直方向上。
- 起点(0, 0),代表我们还没有对字符串 a、b 进行任何编辑操作(删除、插入、保持不动)。
- 图中的任一条线段,代表一个编辑操作
- 水平线段:表示删除字符串 a 中的一个字符(线段终点所指字符)。例如:从 (0, 0) 移动到 (1, 0),代表删除字符串 a 中的字符 A。
- 竖直线段:表示插入字符串 b 中的一个字符(线段终点所指字符)。例如:从 (0, 0) 移动到 (0, 1),代表插入字符串 b 中的字符 C。
- 对角线段:保持 a、b 对应位置上的字符不动(因为同时删除、插入相同的一个字符)。例如:从 (2, 0) 移动到 (3, 1),代表保持字符 C 不变。
- 一步只能走一条线段(水平或竖直)
- 从起点(0, 0)一步一步走到终点(7, 6),代表我们找到了一种将字符串 a 转换为字符串 b 的编辑序列,也即找到了一种字符串 a、b 间的“差异”。

举个例子:下图即代表从逐个删除字符串 a 中的所有字符,然后再逐个插入字符串 b 中的所有字符。
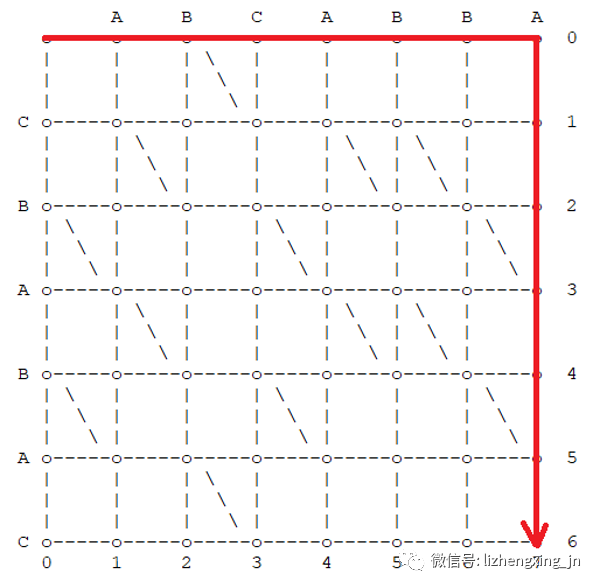

举个例子:下图就是 Myers 算法找到的将字符串 a 转换为字符串 b 的编辑序列。
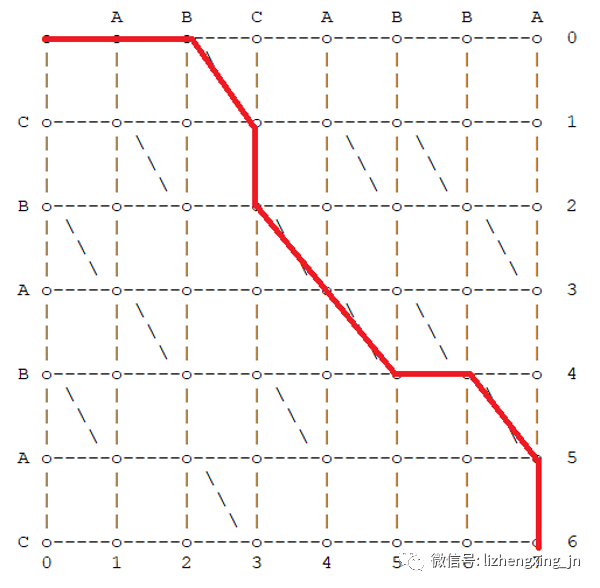

小结一下:从起点(0, 0)到终点(7, 6)的任意一条路径,都是对字符串 a、b 差异的一种解释,即都是一种将字符串 a 转换为字符串 b 的编辑序列。Myers 算法的目标就是找到从起点(0, 0)到终点(7, 6)的一条最优路径。
流程模拟
接下来,我们来模拟一下 Myers 算法的流程,找到从起点(0, 0)到终点(7, 6)的一条最优路径。
- (0, 0)
- 可以选择右移一步到(0, 1)
- 也可以选择下移一步到(0, 1)
- 从(0, 0)点出发,移动一步,有两种可能
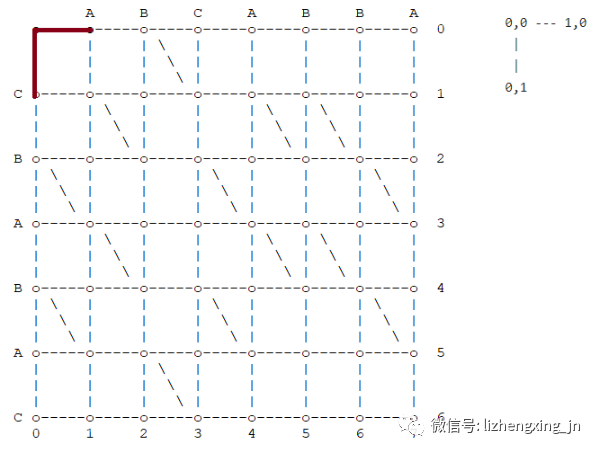
- (0, 1)、(1, 0)
- 向右移动到(2, 0),由于遇到对角线,可以继续移动到(3, 1)
- 向下移动到(1, 1),由于遇到对角线,可以继续移动到(2, 4)
- 向右移动到(1, 1),由于遇到对角线(它不产生编辑操作),所以可以直接移动到(2, 2)
- 向下移动到(0, 2),由于遇到对角线(它不产生编辑操作),所以可以直接移动到(2, 4)
- 从(0, 1)出发,有两种可能
- 从(1, 0)出发,有两种可能
- 需要注意,(2, 4)可以从(0, 1)或(1, 0)移动过来,因为我们偏向于删除操作优先,所以我们优先选择(2, 4)从(1, 0)移动过来。
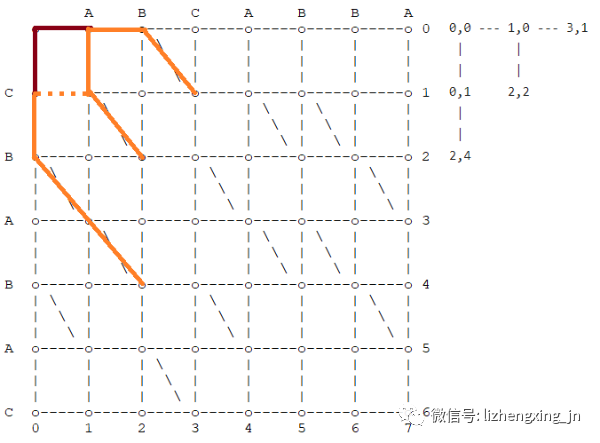
- (2, 4)、(2, 2)、(3, 1)
- 向下移动到(3, 2),由于遇到对角线,可以继续移动到(5, 4)
- 向又移动到(4, 1),由于遇到对角线,可以继续移动到(5, 2)
- 向右移动到(3, 2),由于遇到对角线,可以继续移动到(5, 4)
- 向下移动到(2, 3)
- 向右移动到(3, 4),由于遇到对角线,可以继续移动到(4, 5)
- 向下移动到(2, 5),由于遇到对角线,可以继续移动到(3, 6)
- 从(2, 4)出发,有两种可能
- 从(2, 2)出发,有两种可能
- 从(3, 1)出发,有两种可能
- 需要注意,(5, 4)可以从(2, 2)或(3, 1)移动过来,因为我们偏向于删除操作优先,所以我们优先选择(5, 4)从(3, 1)移动过来。
- 同时注意,到目前为止一共走了 3 步,从(2, 2)往下一步走到(2, 3)是在所有走了 3 步的路径中,距离终点(7, 6)最远的一条路线,基本可以忽略。
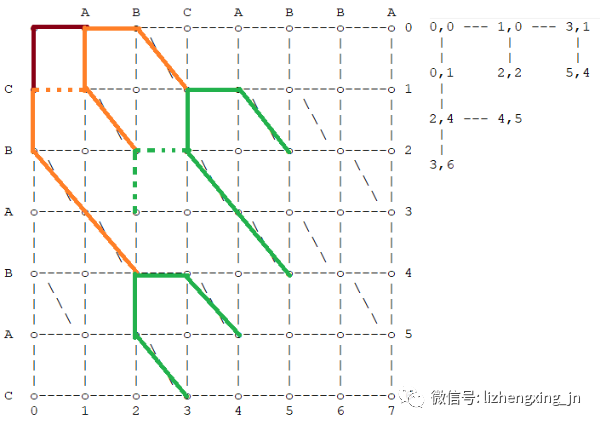
- (3, 6)、(4, 5)、(5, 4)、(5, 2)
- 向右移动到(6, 2),遇到对角线,到(7, 3)
- 向下移动到(5, 3),遇到对角线,到(7, 5)
- 向右移动到(6, 4),遇到对角线,到(7, 5)
- 向下移动到(5, 5)
- 向右移动到(5, 5)
- 向下移动到(4, 6)
- 向右移动到(4, 6)
- 已经到底了,不能向下移动了
- 从(3, 6)出发
- 从(4, 5)出发
- 从(5, 4)出发
- 从(5, 2)出发
- 同理,优先选择(4, 6)从(4, 5)过来;
- 同理,优先选择(5, 5)从(5, 4)过来;
- 对于(7, 5),由于从(5, 4)出发是右移,而从(5, 2)出发是下移,所以优先选择从(5, 4)出发。
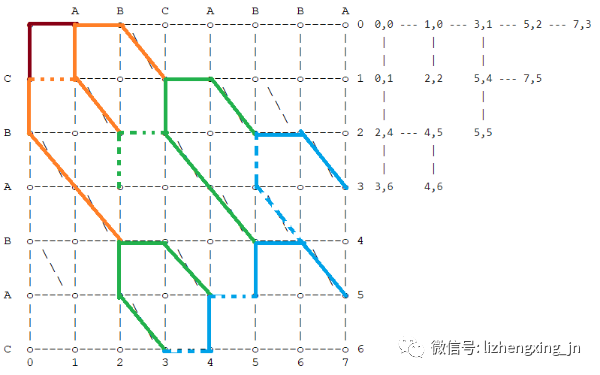
- (4, 6)、(5, 5)、(7, 5)、(7, 3)
- 从图中可以直接看出,(7, 5)往下走一步即到达终点(7, 6)
- 其他的点再走一步,不可能到达终点,所以不予讨论了。
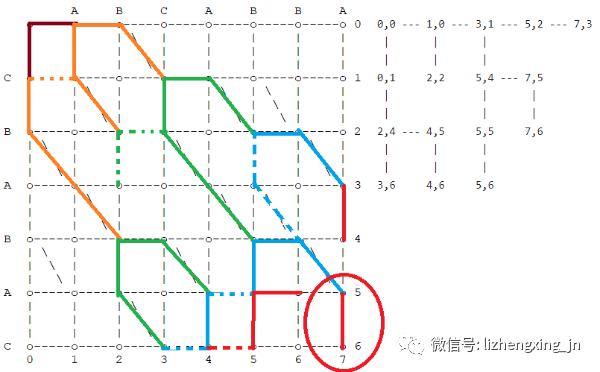
到此,从起点(0, 0)走了 5 步,到达了终点(7, 6)。图中粉色路径就是 Myers 算法找出的字符串 a、b 之间的最短编辑距离,也就是 Myers 算法找出的 a 、b 字符串间的差异。
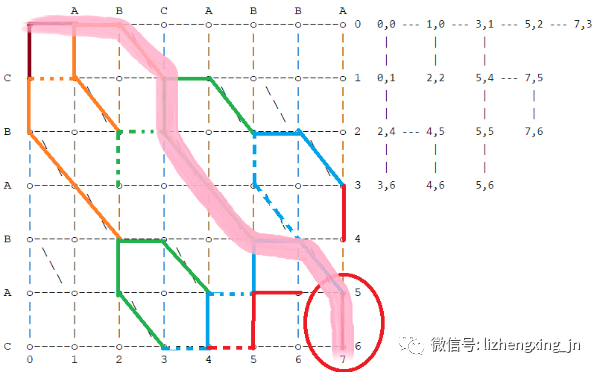

回顾一下找到这条最短路径的过程:
- 这条路径用了最短的步数(5步)。
- 即:这条路径包含了最少数量的横向(代表删除操作)和竖向线段(代表插入操作)。
- 即:这条路径利用了最多的对角线段(因为它代表没有操作,即保持字符不动)。
- 这条路径偏好横向移动(因为我们偏好删除操作优先)。
Myers算法理论
接下来,我们从理论层面,对 Myers 算法进行分析。
再重新回顾一下图中的几个概念:
- 移动一格
- 向右移动一格,代表删除操作,删除字符串 a 中的一个字符(终点位置指向的字符)。
- 向下移动一格,代表插入操作,插入字符串 b 中的一个字符(终点位置指向的字符)。
- 对角移动一格,代表没有操作,既不删除也不插入,保持对应位置字符不动。
- 移动一步
- 可以向右移动一格,如果遇到对角线,可以沿对角线继续移动。
- 可以向下移动一格,如果遇到对角线,可以沿对角线继续移动。
让我们换个视角,从步数(深度)维度来观察所走过的路线,从起点(0, 0)到终点(7, 6)只走了 5 ,而且每走完一步,会到达图中不同的点,图中所示就是等深(d)线。
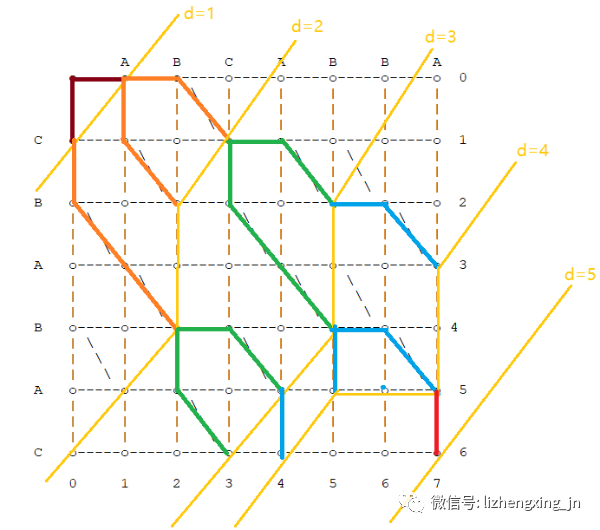
Myers 算法引入了很重的要的一个概念:k 值。
对于任意一点(x, y),我们定义这一点的 k 值为:
k = x - y注意到,处于对角线上的点的 k 值是相同的。下图展示出来的就是等 k 线。
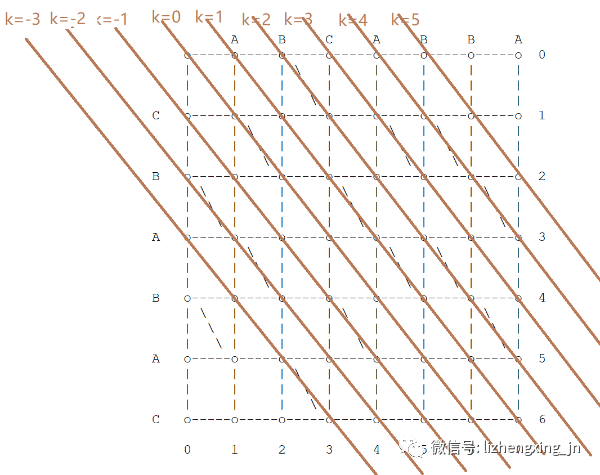
Myers 算法巧妙的地方,就是它把 d(步数或深度) 和 k 紧密联系了起来。
联系1:从起点(0, 0)走出 D 步,只可能会停在 k = {-D, -D+2, ... D-2, D} 线上。
如下图:
- 第 1 步:可能停在 k= {-1, 1} 线上
- 第 2 步:可能停在 k= {-2, 0, 2} 线上
- 第 3 步:可能停在 k= {-3, -1, 1, 3} 线上
- 第 4 步:可能停在 k= {-4, -2, 0, 2, 4} 线上
- 第 5 步:可能停在 k= {-5, -3, -1, 1, 3, 5} 线上
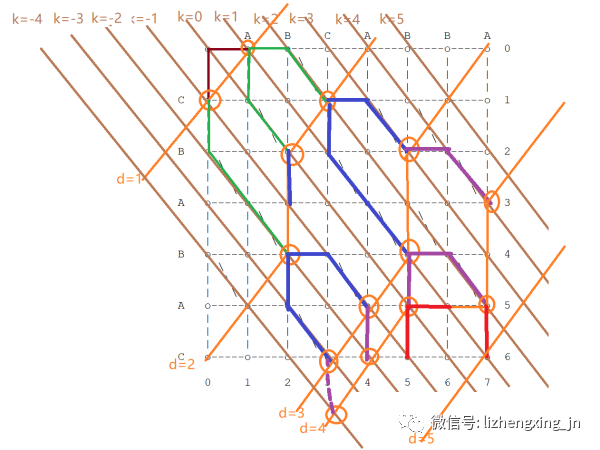
这里只是给大家通过图示建立一下直观认识,论文中使用了数学归纳法对这个结论进行了证明,感兴趣的同学可以自行阅读。
联系2:移动方式和 k 值的变化关系。
仔细观察一下,我们又可以注意到,移动一格和 k 值的变化有如下关系:
- 如果向右移动一格,k 值 +1
- 如果向下移动一格,k 值 - 1
- 如果沿对角线移动,k 值不变。
对于移动一步,我们有:
- 可以向右移动一格(k 值 +1),如果存在对角线,可以沿对角线继续移动(k 值不变)。所以最终结果也是 k 值 +1
- 可以向下移动一格(k 值 -1),如果存在对角线,可以沿对角线继续移动(k 值不变)。所以最终结果也是 k 值 -1
联系3:第 D 步 一定是从第 D-1 步移动 1 步过来的。 (PS:好像是废话😄 )
联系4: (PS:重点来了👀️ )
由于,走到第 D 步,可能会停在 k = {-D, -D+2, ... D-2, D} 线上。
对于走了 d 步、停留在 k 线上的点(我们用坐标(d, k)描述),它一定只可能:
- 从 d - 1步所在的 k - 1线上,右移一步(如果遇到对角线,可以继续沿对角线移动(k 值不变))到达。
- 从 d - 1步所在的 k +1线上,下移一步(如果遇到对角线,可以继续沿对角线移动(k 值不变))到达。
ok,我们沿着这个思路重新模拟一遍流程。
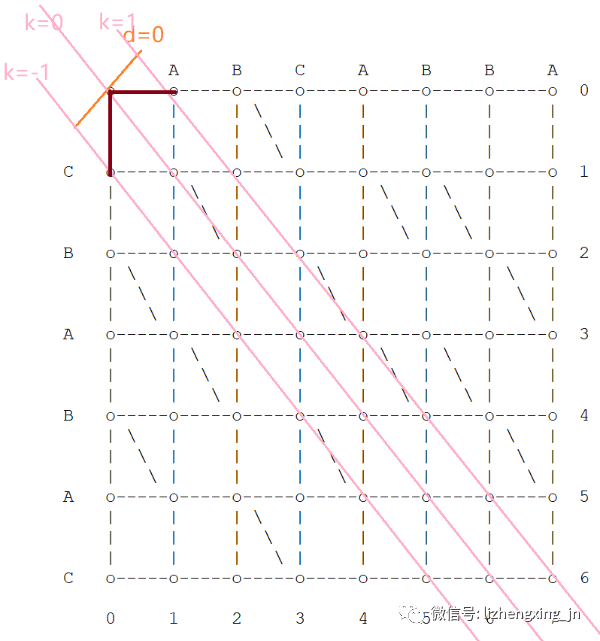
第 0 步:d=0 停在 k=0 线上,位置(0, 0)。
第 1 步:由于 d=1 可能停在 k=-1、k=1线上
- 如果 k=-1
- 它不可能从d=0、k-1=-2线右移一步过来。(看图,因为越界了😄 )
- 它可能从 d=0、k+1=0 的(0, 0)下移一步到达(0, 1)。
- 如果k=1
- 它可能从 d=0、k-1=0的(0, 0)右移一步到达(1, 0)。
- 它不可能从d=0、k+1=2线下移一步过来。(看图,因为越界了😄 )
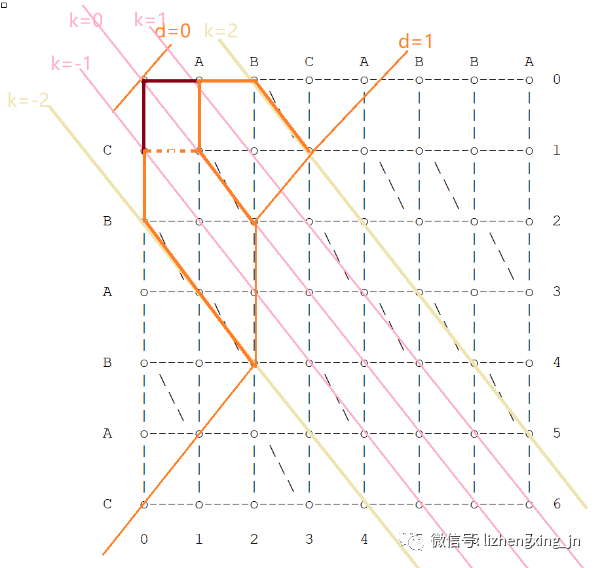
第 2 步:由于 d=2 可能停在 k=-2、k=0、k=2线上
- 如果 k=-2
- 它不可能从d=1、k-1=-3线右移一步过来。(看图,因为越界了😄 )
- 它可能从 d=1、k+1=-1的(0, 1)下移一步到(0, 2),沿对角线可继续移动到(2, 4)
- 如果 k=0
- 注:因为我们偏向于优先进行删除操作随后插入操作,所以对于 k=0,我门偏向于从k+1=1的(1, 0)移动到(2, 2)(注:因为k+1=1的(1,0)在k-1=-1的(0, 1)的右侧)。
- 它可能从 d=1、k-1=-1的(0, 1)右移一步到(1, 1),沿对角线可继续移动到(2, 2)
- 它可能从 d=1、k+1=1的(1, 0)下移一步到(1, 1),沿对角线可继续移动到(2, 2)
- 如果 k=2
- 它可能从 d=1、k-1=1的(1, 0)右移一步到(2, 0),沿对角线可继续移动到(3, 1)
- 它不可能从d=1、k+1=3线下移一步过来。(看图,因为越界了😄 )
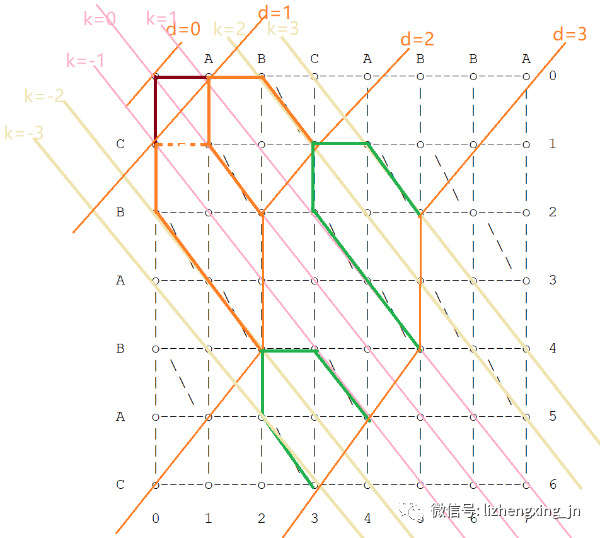
第 3 步:由于 d=3 可能停在 k=-3、k=-1、k=1、k=3线上
- 如果 k=-3
- 它只可能从d=2、k+1=-2 的(2, 4)下移一步到(2,5),沿对角线移动到(3, 6)
- 如果 k=-1
- 两者起点的横坐标都是2,而且因为我们偏好保留连续的删除操作,所以我们从(2, 4)继续右移到(3, 4),然后沿对角线移动到(4, 5)
- 它可能从 d=2、k-1=-2 的(2, 4)右移
- 它可能从 d=2、k+1=0 的(2, 2)下移
- 如果 k=1
- 由于k+1=2的横坐标比较大,所以我们选择从(3, 1)下移到(3, 2),然后沿对角线移动到(5, 4)
- 它可以从 d=2、k-1=0的(2, 2)右移
- 它可能从 d=2、k+1=2 的(3, 1)下移
- 如果 k=3
- 它只可以从 d=2、k-1=2的(3, 1)右移到(4, 1),然后沿对角线移动到(5, 2)
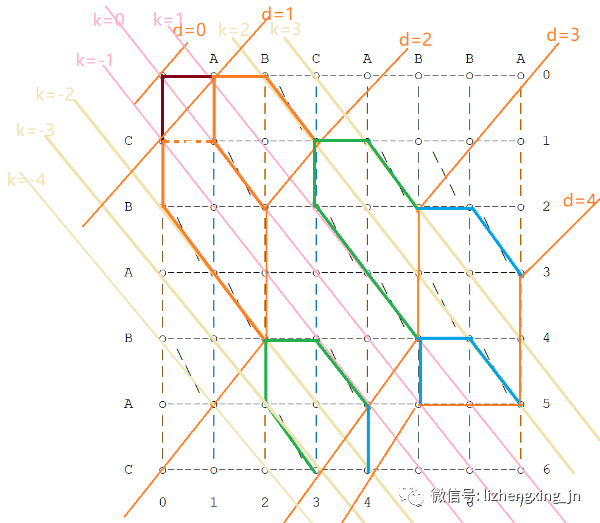
第 4 步:由于 d=4 可能停在 k=-4、k=-2、k=0、k=2、k=4线上
- 如果 k=-4
- 从图中可以看出,k=-4时不用考虑(越界了...👀️ )
- 如果 k=-2
- 由于k+1=2的横坐标 4 比较大,所以我们选择从(4, 5)下移到(4, 6)
- 它可以从 d=3、k-1=-3的(3, 6)右移
- 它可能从 d=3、k+1=-1 的(4, 5)下移
- 如果 k=0
- 由于k+1=1的横坐标 5 比较大,所以我们选择从(5, 4)下移到(5, 5)
- 它可以从 d=3、k-1=-1的(4, 5)右移
- 它可能从 d=3、k+1=1 的(5, 4)下移
- 如果 k=2
- 两者起点的横坐标都是5,而且因为我们偏好保留连续的删除操作,所以我们从(5, 4)继续右移到(6, 4),然后沿对角线移动到(7, 5)
- 它可以从 d=3、k-1=1的(5, 4)右移
- 它可能从 d=3、k+1=3 的(5, 2)下移
- 如果 k=4
- 它只可能从 d=3、k-1=3的(5, 2)右移到(6, 2),然后沿对角线到(7, 3)
第 5 步:由于 d=5 可能停在 k=-5、k=-3、k=-1、k=1、k=4、k=5线上
- 如果 k=-5、k=-3
- 从图中可以看出,k=-5、k=-3时不用考虑(越界了...👀️ )
- 如果 k=-1
- 由于k+1=0的横坐标 5 比较大,所以我们选择从(5, 5)下移到(5, 6)
- 它可以从 d=4、k-1=-2的(4, 6)右移
- 它可能从 d=4、k+1=0 的(5, 5)下移
- 如果 k=1
- 由于k+1=2的横坐标 7 比较大,所以我们选择从(7, 5)下移到(7, 6),到达终点!!!!
- 它可以从 d=4、k-1=0的(5, 5)右移
- 它可能从 d=4、k+1=2 的(7, 5)下移
- 如果 k=3
- 它只可能从 d=3、k+1=4的(7, 3)下移到(7, 4)
- 如果 k=5
- 越界了,不用考虑...
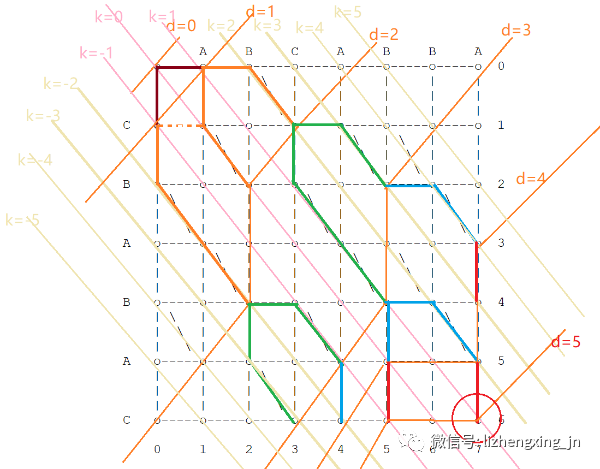
至此,我们使用 Myers 算法找了一条从起点(0,0)到终点(7,6)的最短路径。
Myers算法程序
下面让我们把上面的算法流程,转换为可运行代码。
计算这条最短路径的深度
因为 从起点(0, 0)出发走出 d 步时,它只可能落在 k={-d, -d+2, ...., d-2, d} 的 k 线上。
所以我们算法的本质上是,在走出一步后,计算这一步可能落在的每条 k 线上的最远位置,一直到碰到终点为止。
首先,对于字符串 a、b,它们的长度分别为 N、M,那么这个最短路径的深度上限为:N + M。(例如:当字符串a、b间没有任何公共元素时,只能把字符串 a 中的所有字符逐个删除,然后逐个插入字符串 b 中的所有字符。🚀️ )
const N = a.length;
const M = b.length;
const MAX = N + M;
for (let d = 0; d <= MAX; d++) {
...
}其次,走到第 d 步时,落点只可能在 k={-d, -d+2, ...., d-2, d} 的 k 线上,所以我们只需要计算在这几条 k 线上能在图中走到什么位置(x, y)。
const N = a.length;
const M = b.length;
const MAX = N + M;
for (let d = 0; d <= MAX; d++) {
for (let k = -d; k <= d; k = k + 2) {
let x, y;
.... // 计算走到 d 步,各 k 线上可能走到的位置(x, y)
}
}到这里,有没有注意到,我们关注的实际上是:d、k、(x, y)间的关系;
技巧1🚀️ :
因为:k = x - y
所以:我们只需要关注(或者说存储):d、k、x 间的关系即可。 (PS:因为 y 可以由 x - k 推出。)
到此,可以用一个二维数组来描述 d、k、x 间的关系:
d | k | k | |||||
|---|---|---|---|---|---|---|---|
0 | 0 | ||||||
1 | -1 | 1 | |||||
2 | -2 | 0 | 2 | ||||
3 | -3 | -1 | 1 | 3 |
技巧2🚀️ :
因为,走到第 d 步时,落点只可能在 k={-d, -d+2, ...., d-2, d} 的 k 线上。
所以当 d 是偶数时,落点也是在偶数 k 线上;当 d 是奇数是,落点在奇数 k 线上。
并且,走到第 d 步所处的 k 线,只能:
- 从 d - 1 步的 k-1 线右移(如果有对角线,继续沿对角线移动)到达。
- 从 d +1 步的 k+1 线下移(如果有对角线,继续沿对角线移动)到达。
也就是说,走到第 d 步,至于 d - 1步有关系,与 d-2、d-3等前面的步骤没有关系。
并且,d 与 d-1,d-1与d-2 ..... 每一对的奇偶数是错开的。
所以,上面的二维数组,可以用一个一维数组替代。
因为,d 的最大数值是 N + M,所以 k 最大范围是 -(N+M) ~ (N+M)。
所以,程序可以简化为:
const N = a.length;
const M = b.length;
const MAX = N + M;
const v: number[] = new Array(2 * MAX + 1).fill(-1);
for (let d = 0; d <= MAX; d++) {
for (let k = -d; k <= d; k = k + 2) {
let x, y;
.... // 计算走到 d 步,各 k 线上可能走到的位置(x, y)
}
}下面我们就需要根据d、k来计算 x:
因为,走到第 d 步所处的 k 线,只能:
- 从 d - 1 步的 k-1 线右移(如果有对角线,继续沿对角线移动)到达。
- 从 d +1 步的 k+1 线下移(如果有对角线,继续沿对角线移动)到达。
- 而且不能跨越边界(例如:k==-d时,只能从 k+1下移;k==d时,只能从k-1右移)。
- 而且我们偏向保留最多的连续删除操作(我们会观察 v[k+1]和v[k-1]间的大小)。
所以,综合上面所有的信息,就得到:
private shortest_edit(
a: Array<T>,
b: Array<T>
): [number, number, Array<number[]>] {
const N = a.length;
const M = b.length;
const MAX = N + M;
const v: number[] = new Array(2 * MAX + 1).fill(-1);
const vHis: Array<number[]> = [];
v[1] = 0;
for (let d = 0; d <= MAX; d++) {
vHis.push([...v]);
for (let k = -d; k <= d; k = k + 2) {
let x, y;
if (k == -d || (k != d && this.getX(v, k - 1) < this.getX(v, k + 1))) {
x = this.getX(v, k + 1);
} else {
x = this.getX(v, k - 1) + 1;
}
y = x - k;
while (x < N && y < M && this.equals(a[x], b[y])) {
x++;
y++;
}
this.setX(v, k, x);
if (x >= N && y >= M) {
return [d, k, vHis];
}
}
}
throw new Error("(d, k) not found!");
}根据深度回溯出这条虽短路径
private backTrack(
a: Array<T>,
b: Array<T>,
d: number,
k: number,
vHis: Array<number[]>
) {
const trace: Array<[[number, number], [number, number]]> = [];
// 起点是终点(N, M)
let x = a.length;
let y = b.length;
vHis.reverse().forEach((v) => {
const k = x - y;
let prev_k;
if (k == -d || (k != d && this.getX(v, k - 1) < this.getX(v, k + 1))) {
prev_k = k + 1;
} else {
prev_k = k - 1;
}
const prev_x = this.getX(v, prev_k);
const prev_y = prev_x - prev_k;
while (x > prev_x && y > prev_y) {
trace.push([
[x - 1, y - 1],
[x, y],
]);
x = x - 1;
y = y - 1;
}
if (d > 0) {
trace.push([
[prev_x, prev_y],
[x, y],
]);
}
d--;
x = prev_x;
y = prev_y;
});
return trace;
}根据路径生成比对差异
这一部分相对比较简单,根据上一步计算出的最短路径,并利用基本原则:
- 横向移动一格(y 相同),代表删除(delete)字符串 a 中的一个字符。
- 竖向移动一个(x 相同),代表插入(insert)字符串 b 中的一个字符。
- 对角线移动,表示字符保持不变(equal)。
private makeDiff(
trace: Array<[[number, number], [number, number]]>,
a: Array<T>,
b: Array<T>
) {
const diff: Array<
{
operation: "insert" | "delete" | "equal";
} & E
> = [];
trace.forEach((t) => {
const prev_x = t[0][0];
const prev_y = t[0][1];
const x = t[1][0];
const y = t[1][1];
const a_ele = a[prev_x];
const b_ele = b[prev_y];
if (x == prev_x) {
diff.unshift({
operation: "insert",
...this.str(b_ele),
});
} else if (y == prev_y) {
diff.unshift({
operation: "delete",
...this.str(a_ele),
});
} else {
diff.unshift({
operation: "equal",
...this.str(a_ele),
});
}
});
return diff;
}完整代码
class MyersDiff<T, E> {
equals: (ele_a: T, ele_b: T) => boolean;
str: (ele: T) => E;
constructor(equals: (ele_a: T, ele_b: T) => boolean, str: (ele: T) => E) {
this.equals = equals;
this.str = str;
}
private getX(v: number[], k: number) {
if (k < 0) {
return v[v.length + k];
} else {
return v[k];
}
}
private setX(v: number[], k: number, x: number) {
if (k < 0) {
v[v.length + k] = x;
} else {
v[k] = x;
}
}
private shortest_edit(
a: Array<T>,
b: Array<T>
): [number, number, Array<number[]>] {
const N = a.length;
const M = b.length;
const MAX = N + M;
const v: number[] = new Array(2 * MAX + 1).fill(-1);
const vHis: Array<number[]> = [];
v[1] = 0;
for (let d = 0; d <= MAX; d++) {
vHis.push([...v]);
for (let k = -d; k <= d; k = k + 2) {
let x, y;
if (k == -d || (k != d && this.getX(v, k - 1) < this.getX(v, k + 1))) {
x = this.getX(v, k + 1);
} else {
x = this.getX(v, k - 1) + 1;
}
y = x - k;
while (x < N && y < M && this.equals(a[x], b[y])) {
x++;
y++;
}
this.setX(v, k, x);
if (x >= N && y >= M) {
return [d, k, vHis];
}
}
}
throw new Error("(d, k) not found!");
}
private backTrack(
a: Array<T>,
b: Array<T>,
d: number,
k: number,
vHis: Array<number[]>
) {
const trace: Array<[[number, number], [number, number]]> = [];
// 起点是终点(N, M)
let x = a.length;
let y = b.length;
vHis.reverse().forEach((v) => {
const k = x - y;
let prev_k;
if (k == -d || (k != d && this.getX(v, k - 1) < this.getX(v, k + 1))) {
prev_k = k + 1;
} else {
prev_k = k - 1;
}
const prev_x = this.getX(v, prev_k);
const prev_y = prev_x - prev_k;
while (x > prev_x && y > prev_y) {
trace.push([
[x - 1, y - 1],
[x, y],
]);
x = x - 1;
y = y - 1;
}
if (d > 0) {
trace.push([
[prev_x, prev_y],
[x, y],
]);
}
d--;
x = prev_x;
y = prev_y;
});
return trace;
}
private makeDiff(
trace: Array<[[number, number], [number, number]]>,
a: Array<T>,
b: Array<T>
) {
const diff: Array<
{
operation: "insert" | "delete" | "equal";
} & E
> = [];
trace.forEach((t) => {
const prev_x = t[0][0];
const prev_y = t[0][1];
const x = t[1][0];
const y = t[1][1];
const a_ele = a[prev_x];
const b_ele = b[prev_y];
if (x == prev_x) {
diff.unshift({
operation: "insert",
...this.str(b_ele),
});
} else if (y == prev_y) {
diff.unshift({
operation: "delete",
...this.str(a_ele),
});
} else {
diff.unshift({
operation: "equal",
...this.str(a_ele),
});
}
});
return diff;
}
diff(a: Array<T>, b: Array<T>) {
const [d, k, vHis] = this.shortest_edit(a, b);
const trace = this.backTrack(a, b, d, k, vHis);
const diff = this.makeDiff(trace, a, b);
return diff;
}
}Myers算法示例
最后,用上面复刻出来的 Myers 算法,来复现一下对字符串 a、b 之间的差异比较。
const myers = new MyersDiff<string, { ele: string }>(
(ele_a, ele_b) => {
return ele_a === ele_b;
},
(ele) => {
return {
ele,
};
}
);
const a = "ABCABBA";
const b = "CBABAC";
const diff = myers.diff(a.split(""), b.split(""));
console.log(JSON.stringify(diff, null, 4));
正确,运行出来的结果更预期一致。
参考
The Myers diff algorithm(James Coglan):
- https://blog.jcoglan.com/2017/02/12/the-myers-diff-algorithm-part-1/
- https://blog.jcoglan.com/2017/02/15/the-myers-diff-algorithm-part-2/
- https://blog.jcoglan.com/2017/02/17/the-myers-diff-algorithm-part-3/
Investigating Myers' Diff Algorithm(Nicholas Butler):
- https://www.codeproject.com/Articles/42279/Investigating-Myers-diff-algorithm-Part-1-of-2
- https://www.codeproject.com/Articles/42280/Investigating-Myers-Diff-Algorithm-Part-2-of-2
paper:
- http://www.xmailserver.org/diff2.pdf
misc:
- https://blog.robertelder.org/diff-algorithm/
- https://epxx.co/artigos/diff_en.html
- https://git-scm.com/docs/diff-options